Shape difference

Shape difference matrix based inference following Lele and Cole (1996).

Usage

edma_sdm(a, b, log=TRUE, size=TRUE, edge = NULL)
get_sdm(object, ...)
# S3 method for edma_sdm
get_sdm(object, sort=FALSE,
    level = 0.95, ...)

# S3 method for edma_sdm
print(x, level = 0.95, ...)
Z_test(object, ...)
# S3 method for edma_sdm
Z_test(object, level = 0.95, ...)
# S3 method for edma_sdm
landmarks(x, ...)
# S3 method for edma_sdm
dimensions(x, ...)

# S3 method for edma_sdm
confint(object, parm, level=0.95, ...)
# S3 method for edma_sdm
get_influence(object, statistic=c("Z", "C"),
    level=0.95, ...)

plot_Ztest(x, ...)
# S3 method for edma_sdm
plot_Ztest(x, statistic=c("Z", "C"),
    level = 0.95, ...)

Arguments

a, b: EDMA fit object to compare shapes.
x, object: a SDM object.
log: logical, if form matrix is to be log transformed before calculating the differences.
size: logical, if size difference (C) is to be estimated (TRUE) of fixed as 1 (FALSE).
edge: numeric or character, numeric IDs or the name of the 2 landmarks to be used to calculate C (C=db/da, where da and db are the edge distances between the two landmarks for object a and b respectively). C is calculated using total least squares (TLS) when edge=NULL.
sort: logical, if stacked distances are to be sorted, see Examples.
level: numeric, between 0 and 1, alpha level for confidence interval.
parm: a specification of which parameters are to be given confidence intervals, either a vector of numbers or a vector of names. See confint.
statistic: character, the Z or C statistic to be plotted.
...: other arguments passed to other functions.

Details

Shape difference matrix (SDM) is defined as the difference between the scaled form matrices S(A) and S(B). S(A) = C * FM(A), S(B) = FM(B), where C is a scaling factor and is calculated using total least squares (TLS). Shape difference matrix is S(A) - S(B) when log=FALSE and log(S(A)) - log(S(B)) when log=TRUE.

Inference and visualization is similar to how it is done for FDMs.

Note: the original implementation is usinga particular edge to calculate the size (C) parameter (size=TRUE and edge not NULL). edge=NULL uses total least squares to estimate C based on all the edges of all the landmarks. When size=FALSE we set C=1, assuming sizez are the same.

Value

edma_sdm compares 2 EDMA fit objects and calculates SDM.

References

Lele, S. R., and Cole, T. M. III., 1996. A new test for shape differences when variance-covariance matrices are unequal. Journal of Human Evolution 31:193--212. <doi:10.1006/jhev.1996.0057>

Author

Peter Solymos, Subhash R. Lele, Theodore M. Cole

Examples

file_a <- system.file("extdata/growth/CZP0_wt_global.xyz",
    package="EDMAinR")
file_b <- system.file("extdata/growth/CZP0_mut_global.xyz",
    package="EDMAinR")
l <- c("amsph", "bas", "loci", "lpto", "lsqu",
        "lsyn", "roci", "rpto", "rsqu", "rsyn")

a <- read_xyz(file_a)[l,,]
b <- read_xyz(file_b)[l,,]
a
#> EDMA data: Crouzon unaffected newborn mouse
#> 10 landmarks, 3 dimensions, 11 specimens
b
#> EDMA data: Crouzon mutant newborn mouse
#> 10 landmarks, 3 dimensions, 11 specimens

fit_a <- edma_fit(a, B=10)
fit_b <- edma_fit(b, B=10)

sdm <- edma_sdm(a=fit_a, b=fit_b)
sdm
#> EDMA shape difference matrix
#> Call: edma_sdm(a = fit_a, b = fit_b)
#> 10 bootstrap runs (difference of logarithms)
#> 
#>               2.5%    97.5%
#> Z (shape) -0.12315 0.078195
#> C (scale)  1.00710 1.028947
Z_test(sdm)
#> Bootstrap based EDMA Z-test
#> 10 bootstrap runs
#> 
#>              2.5%   97.5%
#> Z (shape) -0.1232 0.07819
#> C (scale)  1.0071 1.02895
head(confint(sdm))
#>                    2.5%        97.5%
#> bas-amsph  -0.029487476 -0.014229265
#> loci-amsph -0.019440490 -0.007616788
#> lpto-amsph -0.034410862 -0.021164403
#> lsqu-amsph  0.002062971  0.025023641
#> lsyn-amsph -0.017521145  0.004158820
#> roci-amsph -0.016856790 -0.007926380
head(get_sdm(sdm))
#>    row   col         sdm        lower        upper
#> 1  bas amsph -0.02392208 -0.029487476 -0.014229265
#> 2 loci amsph -0.01400145 -0.019440490 -0.007616788
#> 3 lpto amsph -0.02582129 -0.034410862 -0.021164403
#> 4 lsqu amsph  0.01659426  0.002062971  0.025023641
#> 5 lsyn amsph -0.00905969 -0.017521145  0.004158820
#> 6 roci amsph -0.01156002 -0.016856790 -0.007926380
head(get_sdm(sdm, sort=TRUE, decreasing=TRUE))
#>     row  col        sdm      lower      upper
#> 43 rsqu rpto 0.05906804 0.03520501 0.08276183
#> 25 lsqu lpto 0.04367016 0.03568473 0.05877332
#> 31 lsyn lsqu 0.03351607 0.02497865 0.03894468
#> 41 rsqu roci 0.02675907 0.01960036 0.03969825
#> 45 rsyn rsqu 0.02636038 0.00629132 0.03922674
#> 19 lsqu loci 0.02269395 0.01654100 0.02769915
head(get_sdm(sdm, sort=TRUE, decreasing=FALSE))
#>     row  col         sdm       lower       upper
#> 28 rpto lpto -0.07900089 -0.12315127 -0.04698995
#> 13 lsyn  bas -0.04078567 -0.05528032 -0.02692574
#> 39 rsyn lsyn -0.03605782 -0.04651451 -0.01456456
#> 17 rsyn  bas -0.03495021 -0.04455519 -0.02488746
#> 37 rpto lsyn -0.03361166 -0.04205454 -0.02519528
#> 22 rpto loci -0.03326119 -0.04262783 -0.02239645

get_influence(sdm)
#>    landmark       Zdrop       lower      upper
#> 1     amsph -0.08151834 -0.12572159 0.07534861
#> 2       bas -0.07936769 -0.12272631 0.07756928
#> 3      loci -0.07874282 -0.12286096 0.07754190
#> 4      lpto  0.05483618 -0.05046084 0.08010945
#> 5      lsqu -0.07154565 -0.11575993 0.08943609
#> 6      lsyn -0.08022249 -0.12419779 0.07679128
#> 7      roci -0.07798099 -0.12180816 0.08400709
#> 8      rpto -0.04583163 -0.05896161 0.05307541
#> 9      rsqu -0.07155860 -0.11487683 0.02150563
#> 10     rsyn -0.08005630 -0.12393985 0.07696550

plot_Ztest(sdm, "Z")

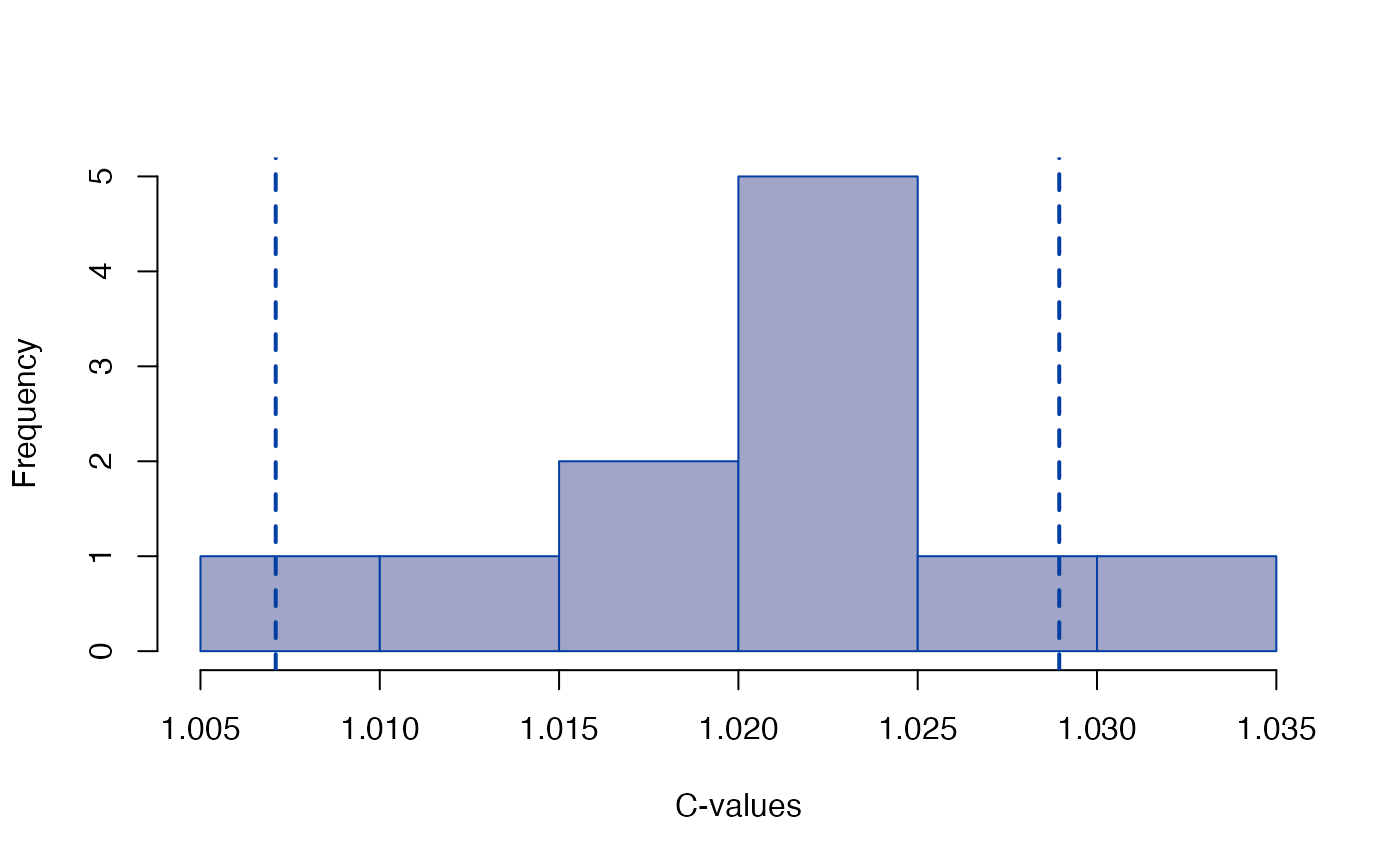
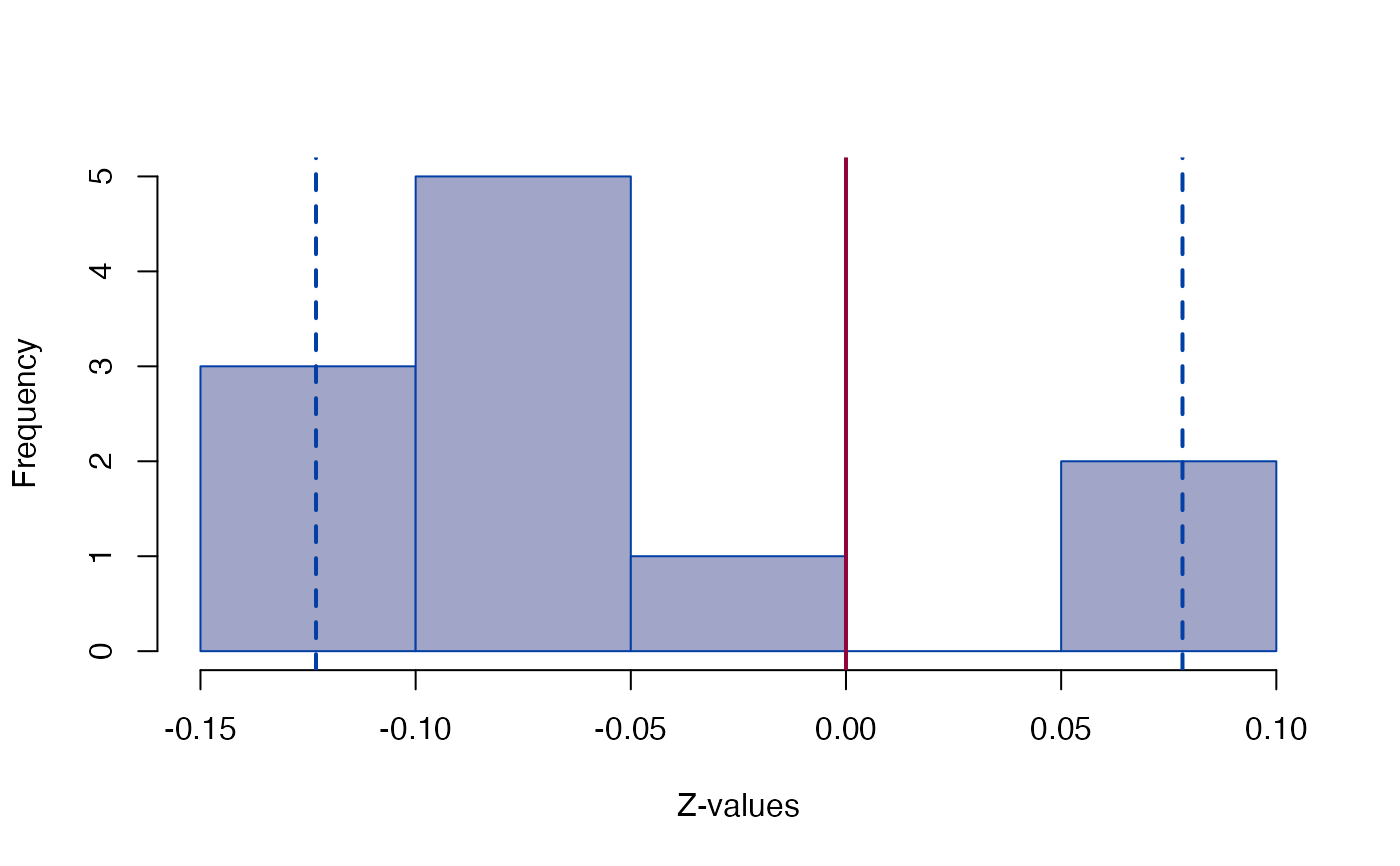plot_Ztest(sdm, "C")

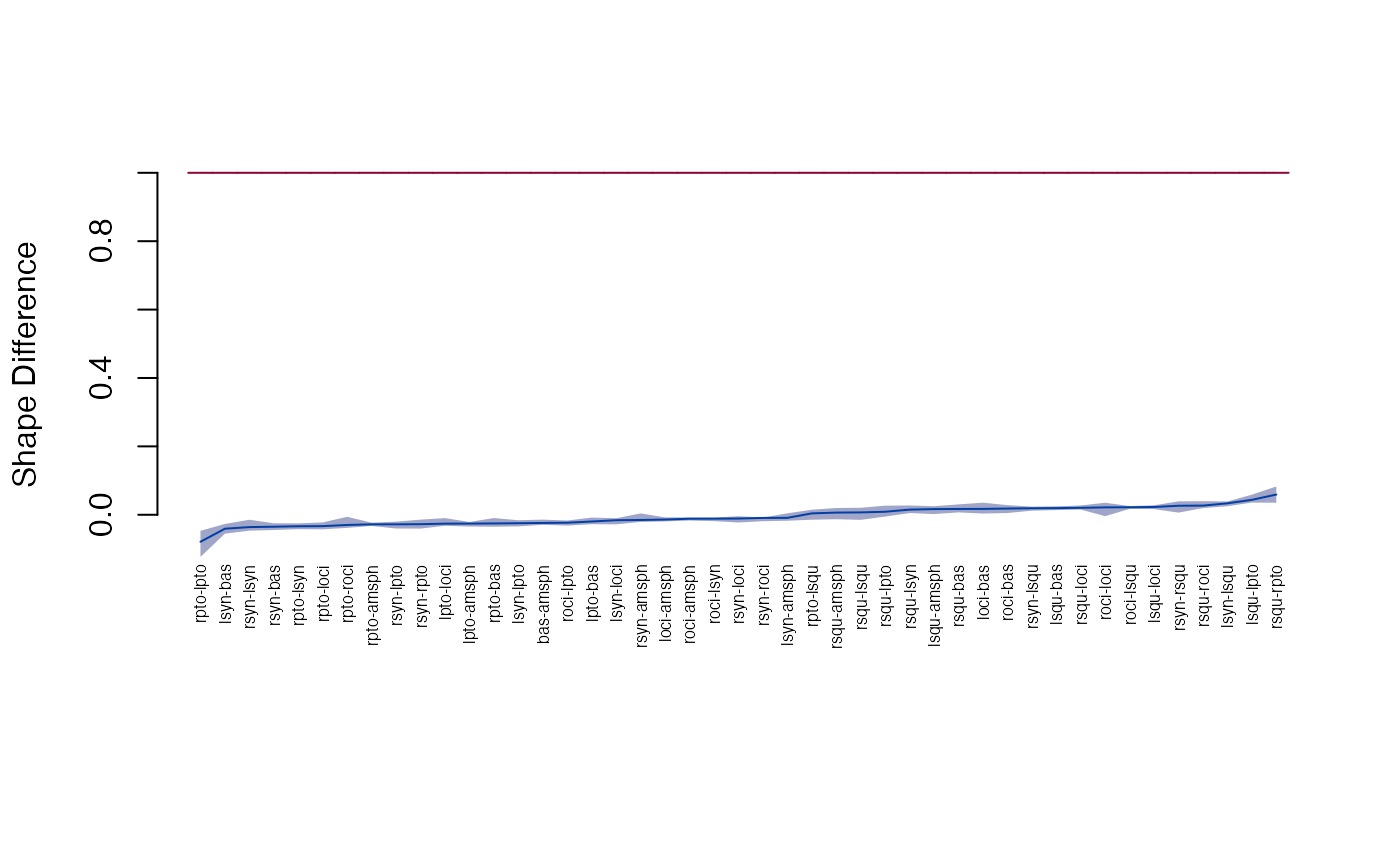
plot_ci(sdm)


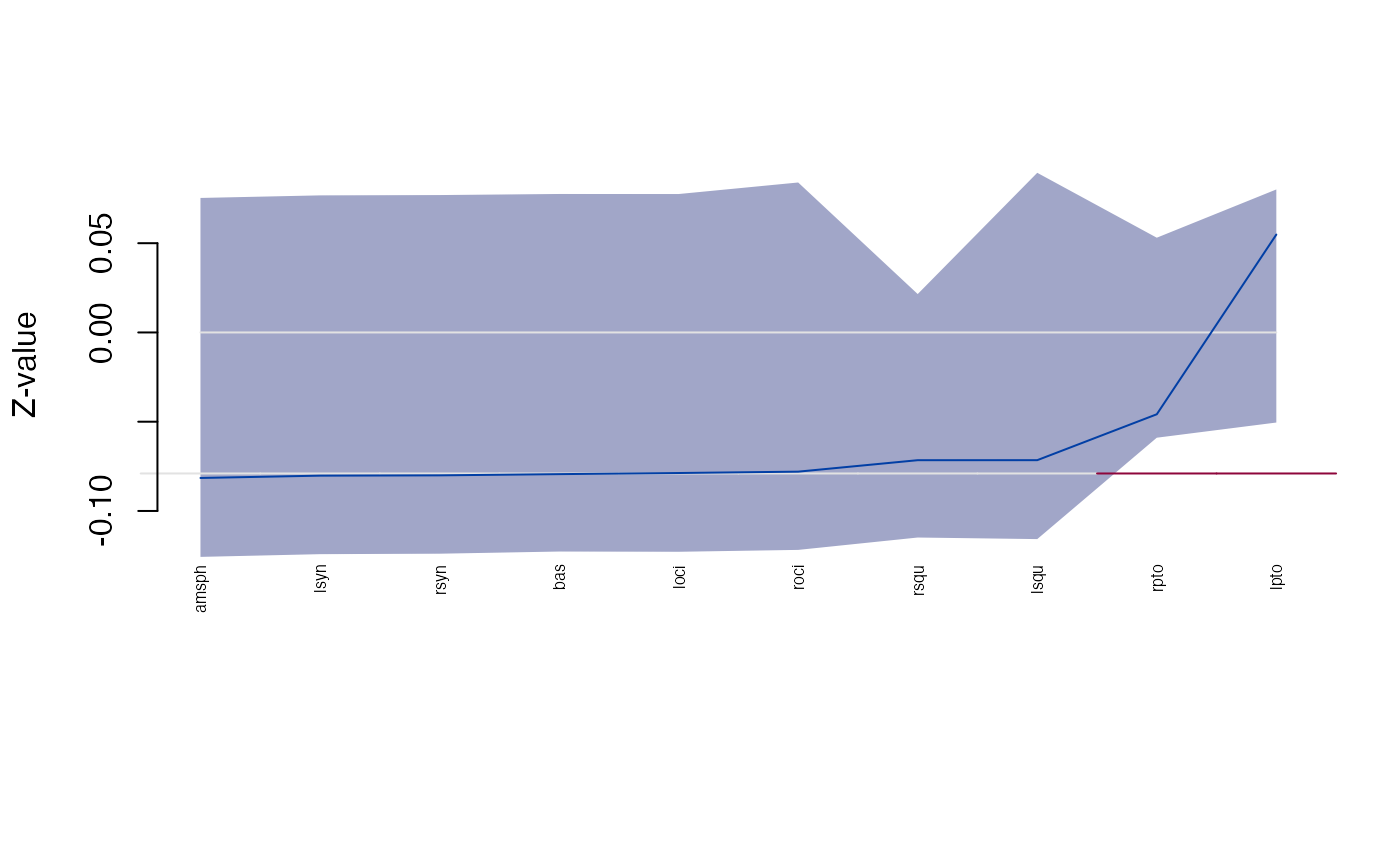
plot(get_influence(sdm))