Péter Sólymos

Progress bar overhead comparisons

October 15, 2016 Code R pbapply progress bar plyr

As a testament to my obsession with progress bars in R, here is a quick investigation about the overhead cost of drawing a progress bar during computations in R. I compared several approaches including my pbapply and Hadley Wickham’s plyr.

Let’s compare the good old lapply function from base R, a custom-made variant called lapply_pb that was proposed here, l_ply from the plyr package, and finally pblapply from the pbapply package:

library(pbapply)
library(plyr)

lapply_pb <- function(X, FUN, ...) {
    env <- environment()
    pb_Total <- length(X)
    counter <- 0
    pb <- txtProgressBar(min = 0, max = pb_Total, style = 3)
    wrapper <- function(...){
        curVal <- get("counter", envir = env)
        assign("counter", curVal +1 ,envir = env)
        setTxtProgressBar(get("pb", envir = env), curVal + 1)
        FUN(...)
    }
    res <- lapply(X, wrapper, ...)
    close(pb)
    res
}

f <- function(n, type = "lapply", s = 0.1) {
    i <- seq_len(n)
    out <- switch(type,
        "lapply" = system.time(lapply(i, function(i) Sys.sleep(s))),
        "lapply_pb" = system.time(lapply_pb(i, function(i) Sys.sleep(s))),
        "l_ply" = system.time(l_ply(i, function(i)
            Sys.sleep(s), .progress="text")),
        "pblapply" = system.time(pblapply(i, function(i) Sys.sleep(s))))
    unname(out["elapsed"] - (n * s))
}

Use the function f to run all four variants. The expected run time is n * s (number of iterations x sleep duration), therefore we can calculate the overhead from the return objects as elapsed minus expected. Let’s get some numbers for a variety of n values and replicated B times to smooth out the variation:

n <- c(10, 100, 1000)
s <- 0.01
B <- 10

x1 <- replicate(B, sapply(n, f, type = "lapply", s = s))
x2 <- replicate(B, sapply(n, f, type = "lapply_pb", s = s))
x3 <- replicate(B, sapply(n, f, type = "l_ply", s = s))
x4 <- replicate(B, sapply(n, f, type = "pblapply", s = s))

m <- cbind(
    lapply = rowMeans(x1),
    lapply_pb = rowMeans(x2),
    l_ply = rowMeans(x3),
    pblapply = rowMeans(x4))

op <- par(mfrow=c(1, 2))
matplot(n, m, type = "l", lty = 1, lwd = 3,
    ylab = "Overhead (sec)", xlab = "# iterations")
legend("topleft", bty = "n", col = 1:4, lwd = 3, text.col = 1:4,
    legend = colnames(m))
matplot(n, m / n, type = "l", lty = 1, lwd = 3,
    ylab = "Overhead / # iterations (sec)", xlab = "# iterations")
par(op)
dev.off()

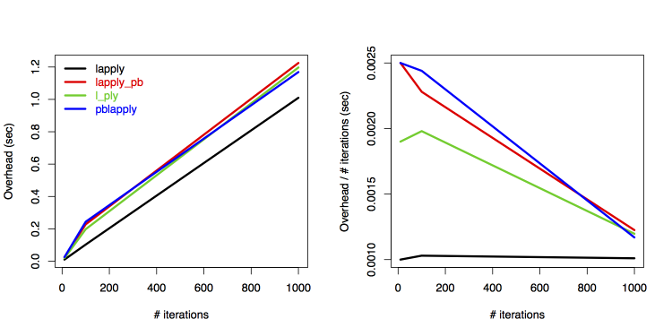
Progress bar overhead

The plot tells us that the overhead increases linearly with the number of iterations when using lapply without progress bar. All other three approaches show similar patterns to each other and the overhead is constant: lines are parallel above 100 iterations after an initial increase. The per iteration overhead is decreasing, approaching the lapply line. Note that all the differences are tiny and there is no practical consequence for choosing one approach over the other in terms of processing times. This is good news and another argument for using progress bar because its usefulness far outweighs the minimal (<2 seconds here for 1000 iterations) overhead cost.

As always, suggestions and feature requests are welcome. Leave a comment or visit the GitHub repo.

Closing the gap between data and decision making

CalgaryR & YEGRUG Meetup: Data Cloning - Hierarchical Models Made Easy

I moved to Canada in 2008 to start a postdoctoral fellowship with Prof. Subhash Lele at the stats department of the University of Alberta. Subhash at the time just published a paper about a statistical technique called data cloning. Data cloning is a way to use Bayesian MCMC algorithms to do frequentist inference. Yes, you read that right.

ABMI (7) ARU (1) Alberta (1) BAM (1) C (1) CRAN (1) Hungary (2) JOSM (2) MCMC (1) PVA (2) PVAClone (1) QPAD (3) R (20) R packages (1) abundance (1) bioacoustics (1) biodiversity (1) birds (2) course (2) data (1) data cloning (4) datacloning (1) dclone (3) density (1) dependencies (1) detect (3) detectability (3) footprint (3) forecasting (1) functions (3) intrval (4) lhreg (1) mefa4 (1) monitoring (2) pbapply (5) phylogeny (1) plyr (1) poster (2) processing time (2) progress bar (4) publications (2) report (1) sector effects (1) shiny (1) single visit (1) site (1) slider (1) slides (2) special (3) species (1) trend (1) tutorials (2) video (4) workshop (1)