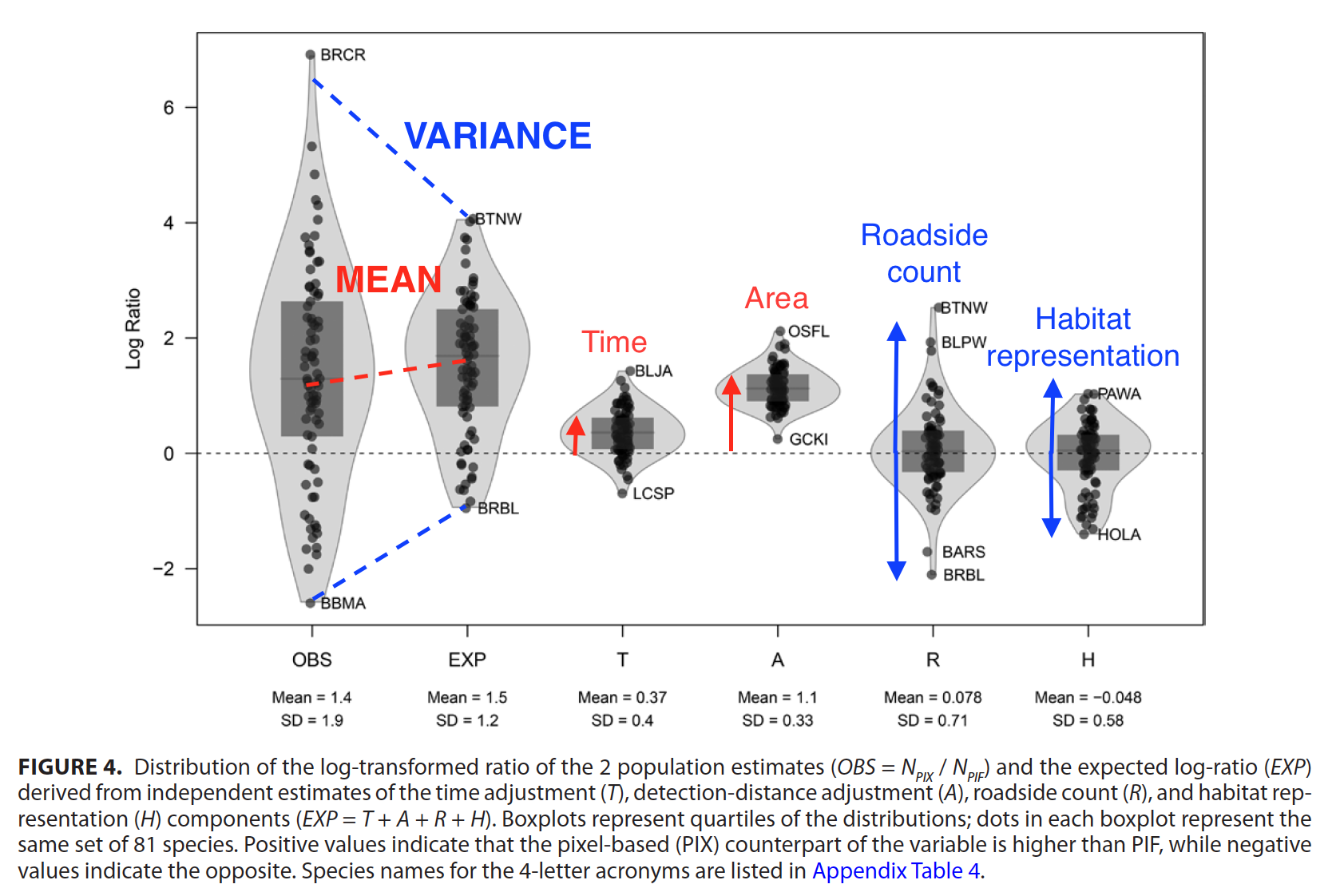
In a paper recently published in the Condor, titled Evaluating time-removal models for estimating availability of boreal birds during point-count surveys: sample size requirements and model complexity, we assessed different ways of controlling for point-count duration in bird counts using data from the Boreal Avian Modelling Project. As the title indicates, the paper describes a cost-benefit analysis to make recommendations about when to use different types of the removal model. The paper is open access, so feel free to read the whole paper here.
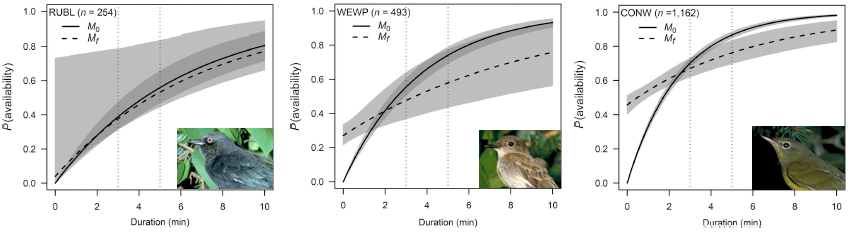
In summary, we evaluated a conventional removal model and a finite mixture removal model, with and without covariates, for 152 bird species. We found that the probabilities of predicted availability under conventional and finite mixture models were very similar with respect to the range of probability values and the shape of the response curves to predictor variables. However, finite mixture models were better supported for the large majority of species. We also found overwhelming support for time-varying models irrespective of the parametrization.
I have written a related post about the journey that led to this paper (Count me in! I am available for detection at 6 AM on May 26th), in this post I describe the math behind the removal modeling as implemented in the detect R package.
Continuous time-removal models
It has long been recognized that nearly all avian field surveys underestimate abundances, unless the estimates are adjusted for the proportion of birds present but undetected at the times and locations surveyed. Detectability is the product of the probability that birds make themselves available for detection by emitting detectable cues (availability); and the probability that an available bird will be perceived by a bird surveyor (perceptibility).
The time-removal model, originally developed for estimating wildlife and fish abundances from mark-recapture studies, was later reformulated for avian surveys with the goal of improving estimates of bird abundance by accounting for the availability bias inherent in point-count data. The removal model applied to point-count surveys estimates the probability that a bird is available for detection as a function of the average number of detectable cues that an individual bird gives per minute (singing rate), and the known count duration.
Time-removal models are based on a removal experiment whereby animals are trapped and thereby removed from the closed population of animals being sampled. When applying a removal model to avian point-count surveys, the counts of singing birds (\(Y_{ij}, \ldots, Y_{iJ}\)) within a given point-count survey \(i\) (\(i = 1,\ldots, n\)) are tallied relative to when each bird is first detected in multiple and consecutive time intervals, with the survey start time \(t_{i0} = 0\), the end times of the time intervals \(t_{ij}\) (\(j = 1, 2,\ldots, J\)), and the total count duration of the survey \(t_{iJ}\). We count each individual bird once, so individuals are ‘mentally removed’ from a closed population of undetected birds by the surveyor.
Data requirements
We have just defined the kind of data we need for the removal models. In this post, I am going to use a data set from our paper about comparing human observer based counts to automated recording units, Paired sampling standardizes point count data from humans and acoustic recorders. The data set we used is wrapped up in an R package called paired (thanks for Steve Van Wilgenburg for suggestions on this post and for agreeing to share this data set).
if (!require(paired))
devtools::install_github("borealbirds/paired")
library(paired)
data(paired)
We will use the counts for Ovenbird, one of the most common species in the data set (abbreviated as "OVEN"). The data is in long format, so I am using the mefa4 R package to make the sample by species cross-tabulation. Then subsetting the data to retain samples obtained by human observers, then getting rid of missing predictor data. For predictors, we will use a variable capturing date (JDAY; standardized ordinal day of the year) and an other one capturing time of day (TSSR; time since local sunrise).
The data frame X contains the predictors. The matrix Y contains the counts of newly counted individuals binned into consecutive time intervals (0–3, 3–5, 5–10 minutes): cell values are the \(Y_{ij}\)’s. The D object is another matrix mirroring the structure of Y
but instead of counts, it contains the interval end times: cell values are
the \(t_{ij}\)’s.
library(mefa4)
spp <- "OVEN"
xt <- Xtab(Count ~ PKEY + Interval, paired,
subset=paired$SurveyType == "HUM" & paired$SPECIES == spp)
Y <- as.matrix(xt[,c("0-3 min", "3-5 min", "5-10 min")])
X <- nonDuplicated(paired[paired$SurveyType == "HUM",],
PKEY, TRUE)[rownames(Y),]
i <- !is.na(X$Latitude)
Y <- Y[i,]
X <- X[i,c("JDAY", "TSSR")]
D <- matrix(c(3, 5, 10), nrow(Y), 3, byrow=TRUE)
dimnames(D) <- dimnames(Y)
tail(X)
## JDAY TSSR
## 96PA-C2-B_2 0.4383562 0.13468851
## 96PA-C2-C_1 0.4438356 0.08526145
## 96PA-C2-C_2 0.4383562 0.15273704
## 96PA-C2-D_1 0.4438356 0.13597129
## 96PA-C2-E_1 0.4438356 0.10122629
## 96PA-C2-F_1 0.4438356 0.11999388
tail(Y)
## 0-3 min 3-5 min 5-10 min
## 96PA-C2-B_2 5 0 0
## 96PA-C2-C_1 2 0 0
## 96PA-C2-C_2 2 0 0
## 96PA-C2-D_1 7 0 0
## 96PA-C2-E_1 2 0 0
## 96PA-C2-F_1 2 0 0
tail(D)
0-3 min 3-5 min 5-10 min
## 96PA-C2-B_2 3 5 10
## 96PA-C2-C_1 3 5 10
## 96PA-C2-C_2 3 5 10
## 96PA-C2-D_1 3 5 10
## 96PA-C2-E_1 3 5 10
## 96PA-C2-F_1 3 5 10
Time-invariant conventional removal model
In the simplest continuous time-removal model, singing events by individual birds are assumed to follow a Poisson process. We can use the rate parameter of the Poisson process (\(\phi\)) to estimate the singing rate of birds during a point count.
In the time-invariant conventional removal model (Me0), the individuals of a species at a given location and time are assumed to be homogeneous in their singing rates. The time to first detection follows the exponential distribution \(f(t_{ij}) = \phi exp(-t_{ij} \phi)\), and the cumulative density function of times to first detection in time interval (0, \(t_{iJ}\)) gives us the probability that a bird sings at least once during the point count as \(p(t_{iJ}) = 1 - exp(-t_{iJ} \phi)\).
We use the cmulti function from the detect R package to fit the removal models. The algorithm used in the function is based on conditional maximum likelihood, and is described in this paper its supporting material.
We are using the type = "rem" for conventional removal models.
library(detect)
Me0 <- cmulti(Y | D ~ 1, X, type="rem")
summary(Me0)
## Call:
## cmulti(formula = Y | D ~ 1, data = X, type = "rem")
##
## Removal Sampling (homogeneous singing rate)
## Conditional Maximum Likelihood estimates
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## log.phi_(Intercept) -0.91751 0.05826 -15.75 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Log-likelihood: -272.1
## BIC = 549.4
Time-varying conventional removal models
Singing rates of birds vary with time of day, time of year, breeding status, and stage of the nesting cycle. Thus, removal model estimates of availability may be improved by accounting for variation in singing rates using covariates for day of year and time of day. In this case \(p(t_{iJ}) = 1 - exp(-t_{iJ} \phi_{i})\) and \(log(\phi_{i}) = \beta_{0} + \sum^{K}_{k=1} \beta_{k} x_{ik}\) is the linear predictor with \(K\) covariates and the corresponding unknown coefficients (\(\beta_{k}\), \(k = 0,\ldots, K\)).
We could fit all the possible multivariate and nonlinear models as we did in the paper, but
let’s just keep it simple for now and fit models with JDAY and TSSR as covariates
(models Me1 and Me2).
Me1 <- cmulti(Y | D ~ JDAY, X, type="rem")
Me2 <- cmulti(Y | D ~ TSSR, X, type="rem")
Now compare the three conventional models based on AIC and inspect the summary for the best supported model with the JDAY effect.
Me_AIC <- AIC(Me0, Me1, Me2)
Me_AIC$dAIC <- Me_AIC$AIC - min(Me_AIC$AIC)
MeBest <- get(rownames(Me_AIC)[Me_AIC$dAIC == 0])
Me_AIC
## df AIC dAIC
## Me0 1 546.1270 0.7187895
## Me1 2 545.4082 0.0000000
## Me2 2 546.4612 1.0529236
summary(MeBest)
## Call:
## cmulti(formula = Y | D ~ JDAY, data = X, type = "rem")
##
## Removal Sampling (homogeneous singing rate)
## Conditional Maximum Likelihood estimates
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## log.phi_(Intercept) 1.460 1.471 0.993 0.321
## log.phi_JDAY -5.235 3.247 -1.612 0.107
##
## Log-likelihood: -270.7
## BIC = 552
To visually capture the time-varying effects, we make some plots using base graphics, colors matching the time-varying predictor. This way we can not only assess how availability probability (given a fixed time interval) is changing with the values of the predictor, but also how the cumulative distribution changes with time.
n <- 100
JDAY <- seq(min(X$JDAY), max(X$JDAY), length.out=n+1)
TSSR <- seq(min(X$TSSR), max(X$TSSR), length.out=n+1)
Duration <- seq(0, 10, length.out=n)
col <- viridis::viridis(n)
b <- coef(MeBest)
op <- par(las=1, mfrow=c(2,1), mar=c(4,4,2,2))
p1 <- 1-exp(-3*exp(b[1]+b[2]*JDAY))
plot(JDAY, p1, ylim=c(0,1), type="n",
main=paste(spp, rownames(Me_AIC)[Me_AIC$dAIC == 0]),
ylab="P(availability)")
for (i in seq_len(n)) {
lines(JDAY[c(i,i+1)], p1[c(i,i+1)], col=col[i], lwd=2)
}
plot(Duration, Duration, type="n", ylim=c(0,1),
ylab="P(availability)")
for (i in seq_len(n)) {
p2 <- 1-exp(-Duration*exp(b[1]+b[2]*JDAY[i]))
lines(Duration, p2, col=col[i])
}
abline(v=3, col="grey")
par(op)
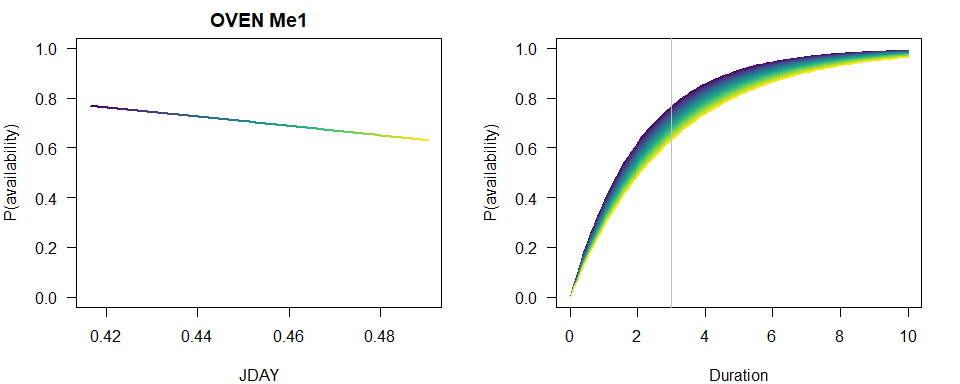
Time-invariant finite mixture removal model
The removal model can also accommodate behavioral heterogeneity in singing by subdividing the sampled population for a species at a given point into a finite mixture of birds with low and high singing rates, which requires the additional estimation of the proportion of birds in the sampled population with low singing rates.
In the continuous-time formulation of the finite mixture (or two-point mixture) removal model, the cumulative density function during a point count is given by \(p(t_{iJ}) = (1 - c) 1 + c [1 - exp(-t_{iJ} \phi)] = 1 - c exp(-t_{iJ} \phi)\), where \(\phi\) is the singing rate for the group of infrequently singing birds, and \(c\) is the proportion of birds during the point count that are infrequent singers. The remaining proportions (\(1 - c\); the intercept of the cumulative density function) of the frequent singers are assumed to be detected instantaneously at the start of the first time interval. In the simplest form of the finite mixture model, the proportion and singing rate of birds that sing infrequently is homogeneous across all times and locations (model Mf0). We are using the type = "fmix" for finite mixture removal models.
Mf0 <- cmulti(Y | D ~ 1, X, type="fmix")
summary(Mf0)
## Call:
## cmulti(formula = Y | D ~ 1, data = X, type = "fmix")
##
## Removal Sampling (heterogeneous singing rate)
## Conditional Maximum Likelihood estimates
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## log.phi_(Intercept) -2.1902 0.4914 -4.457 8.32e-06 ***
## logit.c 0.1182 0.1543 0.766 0.444
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Log-likelihood: -257.6
## BIC = 525.8
Time-varying finite mixture removal models
Previously, researchers (see refs in the paper) have applied covariate effects on the parameter \(\phi_{i}\) of the finite mixture model, similarly to how we modeled these effects in conventional models. This model assumes that the parameter \(c\) is constant irrespective of time and location (i.e. only the infrequent singer group changes its singing behavior).
We can fit finite mixture models with JDAY and TSSR as covariates on \(\phi\)
(models Mf1 and Mf2). In this case \(p(t_{iJ}) = 1 - c exp(-t_{iJ} \phi_{i})\) and \(log(\phi_{i}) = \beta_{0} + \sum^{K}_{k=1} \beta_{k} x_{ik}\) is the linear predictor with \(K\) covariates and the corresponding unknown coefficients (\(\beta_{k}\), \(k = 0,\ldots, K\)).
Mf1 <- cmulti(Y | D ~ JDAY, X, type="fmix")
Mf2 <- cmulti(Y | D ~ TSSR, X, type="fmix")
Compare the three finite mixture models based on AIC and inspect the summary for the best supported model with the TSSR effect in this case.
Mf_AIC <- AIC(Mf0, Mf1, Mf2)
Mf_AIC$dAIC <- Mf_AIC$AIC - min(Mf_AIC$AIC)
MfBest <- get(rownames(Mf_AIC)[Mf_AIC$dAIC == 0])
Mf_AIC
## df AIC dAIC
## Mf0 2 519.2222 0.1053855
## Mf1 3 520.4007 1.2838985
## Mf2 3 519.1168 0.0000000
summary(MfBest)
## Call:
## cmulti(formula = Y | D ~ TSSR, data = X, type = "fmix")
##
## Removal Sampling (heterogeneous singing rate)
## Conditional Maximum Likelihood estimates
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## log.phi_(Intercept) -1.1939 0.4195 -2.846 0.00442 **
## log.phi_TSSR -9.0089 4.7712 -1.888 0.05900 .
## logit.c 0.2016 0.1702 1.184 0.23622
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Log-likelihood: -256.6
## BIC = 529
We produce a similar plot as before.
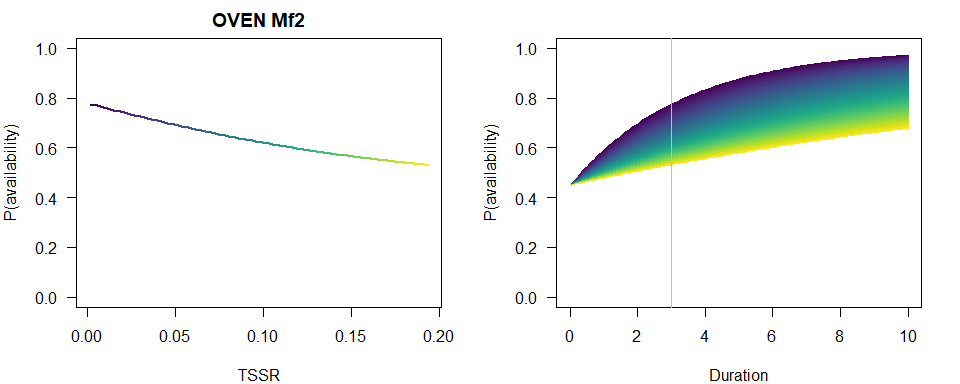
b <- coef(MfBest)
op <- par(las=1, mfrow=c(2,1), mar=c(4,4,2,2))
p1 <- 1-plogis(b[3])*exp(-3*exp(b[1]+b[2]*TSSR))
plot(TSSR, p1, ylim=c(0,1), type="n",
main=paste(spp, rownames(Mf_AIC)[Mf_AIC$dAIC == 0]),
ylab="P(availability)")
for (i in seq_len(n)) {
lines(TSSR[c(i,i+1)], p1[c(i,i+1)], col=col[i], lwd=2)
}
plot(Duration, Duration, type="n", ylim=c(0,1),
ylab="P(availability)")
for (i in seq_len(n)) {
p2 <- 1-plogis(b[3])*exp(-Duration*exp(b[1]+b[2]*TSSR[i]))
lines(Duration, p2, col=col[i])
}
abline(v=3, col="grey")
par(op)
An alternative parametrization is that \(c_{i}\) rather than \(\phi\) be the time-varying parameter, allowing the individuals to switch between the frequent and infrequent group depending on covariates. We can fit this class of finite mixture model with JDAY and TSSR as covariates on \(c\) (models Mm1 and Mm2) using type = "mix" (instead of "fmix"). In this case \(p(t_{iJ}) = 1 - c_{i} exp(-t_{iJ} \phi)\) and \(logit(c_{i}) = \beta_{0} + \sum^{K}_{k=1} \beta_{k} x_{ik}\) is the linear predictor with \(K\) covariates and the corresponding unknown coefficients (\(\beta_{k}\), \(k = 0,\ldots, K\)). Because \(c_{i}\) is a proportion, we model it on the logit scale.
Mm1 <- cmulti(Y | D ~ JDAY, X, type="mix")
Mm2 <- cmulti(Y | D ~ TSSR, X, type="mix")
We did not fit a null model for this parametrization, because it is identical to the Mf0 model, so that model Mf0 is what we use to compare AIC values and inspect the summary for the best supported model with the JDAY effect in this case.
Mm_AIC <- AIC(Mf0, Mm1, Mm2)
Mm_AIC$dAIC <- Mm_AIC$AIC - min(Mm_AIC$AIC)
MmBest <- get(rownames(Mm_AIC)[Mm_AIC$dAIC == 0])
Mm_AIC
## df AIC dAIC
## Mf0 2 519.2222 0.1949952
## Mm1 3 519.0272 0.0000000
## Mm2 3 520.8744 1.8471803
summary(MmBest)
## Call:
## cmulti(formula = Y | D ~ JDAY, data = X, type = "mix")
##
## Removal Sampling (heterogeneous singing rate)
## Conditional Maximum Likelihood estimates
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## log.phi -2.1910 0.4914 -4.459 8.24e-06 ***
## logit.c_(Intercept) -4.7600 3.3828 -1.407 0.159
## logit.c_JDAY 10.7368 7.4287 1.445 0.148
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Log-likelihood: -256.5
## BIC = 528.9
We produce a similar plot as before.
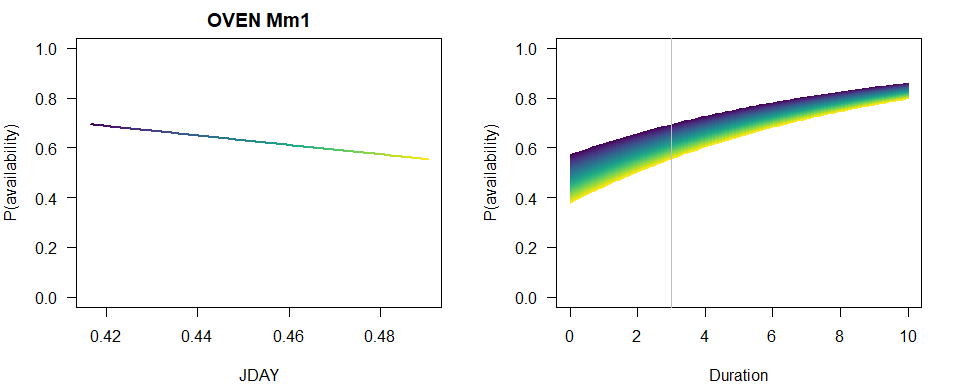
b <- coef(MmBest)
op <- par(las=1, mfrow=c(2,1), mar=c(4,4,2,2))
p1 <- 1-plogis(b[2]+b[3]*JDAY)*exp(-3*exp(b[1]))
plot(JDAY, p1, ylim=c(0,1), type="n",
main=paste(spp, rownames(Mm_AIC)[Mm_AIC$dAIC == 0]),
ylab="P(availability)")
for (i in seq_len(n)) {
lines(JDAY[c(i,i+1)], p1[c(i,i+1)], col=col[i], lwd=2)
}
plot(Duration, Duration, type="n", ylim=c(0,1),
ylab="P(availability)")
for (i in seq_len(n)) {
p2 <- 1-plogis(b[2]+b[3]*JDAY[i])*exp(-Duration*exp(b[1]))
lines(Duration, p2, col=col[i])
}
abline(v=3, col="grey")
par(op)
Let the best model win
So which of the 3 parametrizations proved to be best for our Ovenbird example data? It was the finite mixture with time-varying proportion of infrequent singers with a thin margin. Second was the other finite mixture model, while the conventional model was lagging behind.
M_AIC <- AIC(MeBest, MfBest, MmBest)
M_AIC$dAIC <- M_AIC$AIC - min(M_AIC$AIC)
M_AIC
## df AIC dAIC
## MeBest 2 545.4082 26.38106209
## MfBest 3 519.1168 0.08960974
## MmBest 3 519.0272 0.00000000
Conclusions and applications
Finite mixture models provide some really nice insight into how singing behavior changes over time and, due to more parameters, they provide a better fit and thus minimize bias in population size estimates. But all this improvement comes with a price: sample size requirements (or more precisely, the number of detections required) are really high. To have all the benefits with reduced variance, one needs about 1000 non-zero observations to fit finite mixture models, 20 times more than needed to reliably fit conventional removal models. This is much higher than previously suggested minimum sample sizes.
Our findings also indicate that lengthening the count duration from 3 minutes to 5–10 minutes is an important consideration when designing field surveys to increase the accuracy and precision of population estimates. Well-informed survey design combined with various forms of removal sampling are useful in accounting for availability bias in point counts, thereby improving population estimates, and allowing for better integration of disparate studies at larger spatial scales.
To this end, we provide our removal model estimates as part of the QPAD R package and the R functions required to fit all the above outlined removal models as part of the detect R package. We at the Boreal Avian Modelling Project and our collaborators are already utilizing the removal model estimates to correct for availability bias in our continental and regional projects to inform better management and conservation of bird populations. Read more about these projects in our reports.
Please report any issues here and feel free to comment below!
UPDATE: AOS press release, EurekAlert!, ABMI blog.
]]>