Relational Operators Comparing Values to Intervals

Functions for evaluating if values of vectors are within intervals.

Usage

x %[]% interval
x %)(% interval
x %[<]% interval
x %[>]% interval

x %[)% interval
x %)[% interval
x %[<)% interval
x %[>)% interval

x %(]% interval
x %](% interval
x %(<]% interval
x %(>]% interval

x %()% interval
x %][% interval
x %(<)% interval
x %(>)% interval

intrval_types(type = NULL, plot = FALSE)

Arguments

x: vector or NULL: the values to be compared to interval endpoints.
interval: vector, 2-column matrix, list, or NULL: the interval end points.
type: character, type of operator for subsetting the results. The default NULL means that all types will be displayed.
plot: logical, whether to plot the results, or print a table to the console instead.

Details

Values of x are compared to interval endpoints a and b (a <= b). Endpoints can be defined as a vector with two values (c(a, b)): these values will be compared as a single interval with each value in x. If endpoints are stored in a matrix-like object or a list, comparisons are made element-wise. If lengths do not match, shorter objects are recycled. These value-to-interval operators work for numeric (integer, real) and ordered vectors, and object types which are measured at least on ordinal scale (e.g. dates), see Examples. Note: interval endpoints are sorted internally thus ensuring the condition a <= b is not necessary.

The type argument or the specification of the special function determines the open (( and )) or closed ([ and ]) endpoints and relations.

There are four types of intervals ([], [), (], ()), their negation ()(, )[, ](, ][, respectively), less than ([<], [<), (<], (<)), and greater than ([>], [>), (>], (>)) relations.

Note that some operators return identical results but are syntactically different: %[<]% and %[<)% both evaluate x < a; %[>]% and %(>]% both evaluate x > b; %(<]% and %(<)% evaluate x <= a; %[>)% and %(>)% both evaluate x >= b. This is so because we evaluate only one end of the interval but still conceptually referring to the relationship defined by the right-hand-side interval object and given that a <= b. This implies 2 conditional logical evaluations instead of treating it as a single 3-level ordered factor.

Value

A logical vector, indicating if x is in the specified interval. Values are TRUE, FALSE, or NA (when any of the 3 values (x or endpoints in interval) are NA).

The helper function intrval_types can be used to understand and visualize the operators' effects. It returns a matrix explaining the properties of the operators.

Author

Peter Solymos <solymos@ualberta.ca>

Examples

## motivating example from example(lm)

## Annette Dobson (1990) "An Introduction to Generalized Linear Models".
## Page 9: Plant Weight Data.
ctl <- c(4.17,5.58,5.18,6.11,4.50,4.61,5.17,4.53,5.33,5.14)
trt <- c(4.81,4.17,4.41,3.59,5.87,3.83,6.03,4.89,4.32,4.69)
group <- gl(2, 10, 20, labels = c("Ctl","Trt"))
weight <- c(ctl, trt)
lm.D9 <- lm(weight ~ group)
## compare 95% confidence intervals with 0
(CI.D9 <- confint(lm.D9))
#>                2.5 %    97.5 %
#> (Intercept)  4.56934 5.4946602
#> groupTrt    -1.02530 0.2833003
0 %[]% CI.D9
#> (Intercept)    groupTrt 
#>       FALSE        TRUE 

## comparing dates

DATE <- as.Date(c("2000-01-01","2000-02-01", "2000-03-31"))
DATE %[<]% as.Date(c("2000-01-151", "2000-03-15"))
#> [1]  TRUE FALSE FALSE
DATE %[]% as.Date(c("2000-01-151", "2000-03-15"))
#> [1] FALSE  TRUE FALSE
DATE %[>]% as.Date(c("2000-01-151", "2000-03-15"))
#> [1] FALSE FALSE  TRUE

## interval formats

x <- rep(4, 5)
a <- 1:5
b <- 3:7
cbind(x=x, a=a, b=b)
#>      x a b
#> [1,] 4 1 3
#> [2,] 4 2 4
#> [3,] 4 3 5
#> [4,] 4 4 6
#> [5,] 4 5 7
x %[]% cbind(a, b) # matrix
#> [1] FALSE  TRUE  TRUE  TRUE FALSE
x %[]% data.frame(a=a, b=b) # data.frame
#> [1] FALSE  TRUE  TRUE  TRUE FALSE
x %[]% list(a, b) # list
#> [1] FALSE  TRUE  TRUE  TRUE FALSE

## helper functions

intrval_types() # print
#>          Expression         Visual         Condition      
#> %[]%     x %[]% c(a, b)     ---x===x---    x >= a & x <= b
#> %)(%     x %)(% c(a, b)     ===o---o===    x < a | x > b  
#> %[<]%    x %[<]% c(a, b)    ===o---o---    x < a          
#> %[>]%    x %[>]% c(a, b)    ---o---o===    x > b          
#> %[)%     x %[)% c(a, b)     ---x===o---    x >= a & x < b 
#> %)[%     x %)[% c(a, b)     ===o---x===    x < a | x >= b 
#> %[<)%    x %[<)% c(a, b)    ===o---o---    x < a          
#> %[>)%    x %[>)% c(a, b)    ---o---x===    x >= b         
#> %(]%     x %(]% c(a, b)     ---o===x---    x > a & x <= b 
#> %](%     x %](% c(a, b)     ===x---o===    x <= a | x > b 
#> %(<]%    x %(<]% c(a, b)    ===x---o---    x <= a         
#> %(>]%    x %(>]% c(a, b)    ---o---o===    x > b          
#> %()%     x %()% c(a, b)     ---o===o---    x > a & x < b  
#> %][%     x %][% c(a, b)     ===x---x===    x <= a | x >= b
#> %(<)%    x %(<)% c(a, b)    ===x---o---    x <= a         
#> %(>)%    x %(>)% c(a, b)    ---o---x===    x >= b         
intrval_types(plot = TRUE) # plot


## graphical examples

## bounding box
set.seed(1)
n <- 10^4
x <- runif(n, -2, 2)
y <- runif(n, -2, 2)
iv1 <- x %[]% c(-1, 1) & y %[]% c(-1, 1)
plot(x, y, pch = 19, cex = 0.25, col = iv1 + 1, main = "Bounding box")


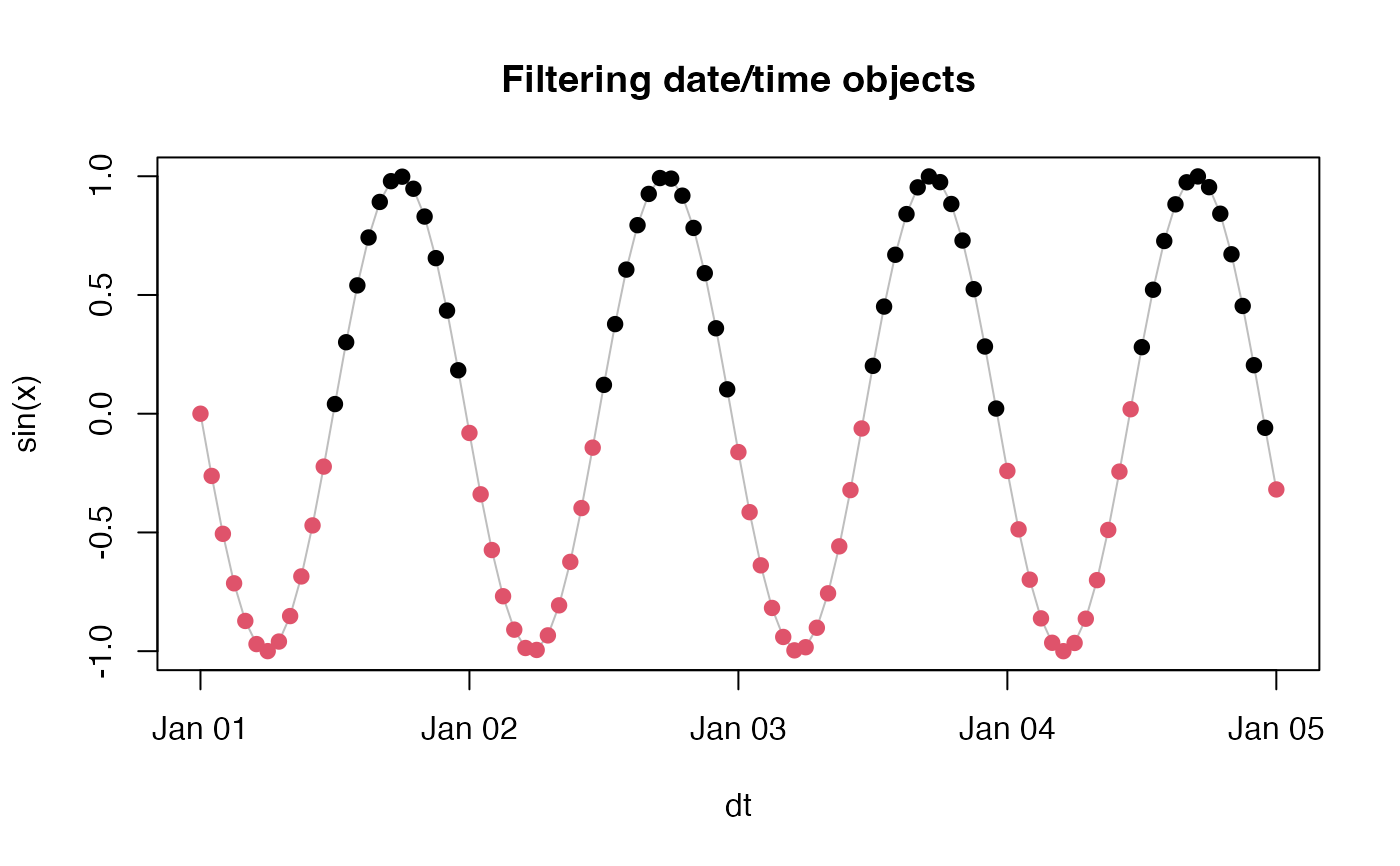
## time series filtering
x <- seq(0, 4*24*60*60, 60*60)
dt <- as.POSIXct(x, origin="2000-01-01 00:00:00")
f <- as.POSIXlt(dt)$hour %[]% c(0, 11)
plot(sin(x) ~ dt, type="l", col="grey",
    main = "Filtering date/time objects")
points(sin(x) ~ dt, pch = 19, col = f + 1)


## watch precedence
(2 * 1:5) %[]% (c(2, 3) * 2)
#> [1] FALSE  TRUE  TRUE FALSE FALSE
2 * 1:5 %[]% (c(2, 3) * 2)
#> [1] 0 0 0 2 2
(2 * 1:5) %[]% c(2, 3) * 2
#> [1] 2 0 0 0 0
2 * 1:5 %[]% c(2, 3) * 2
#> [1] 0 4 4 0 0