Extrapolated Species Richness in a Species Pool

The functions estimate the extrapolated species richness in a species pool, or the number of unobserved species. Function specpool is based on incidences in sample sites, and gives a single estimate for a collection of sample sites (matrix). Function estimateR is based on abundances (counts) on single sample site.

specpool(x, pool, smallsample = TRUE)
estimateR(x, ...)
specpool2vect(X, index = c("jack1","jack2", "chao", "boot","Species"))
poolaccum(x, permutations = 100, minsize = 3)
estaccumR(x, permutations = 100, parallel = getOption("mc.cores"))
# S3 method for poolaccum
summary(object, display, alpha = 0.05, ...)
# S3 method for poolaccum
plot(x, alpha = 0.05, type = c("l","g"), ...)

Arguments

x	Data frame or matrix with species data or the analysis result for `plot` function.
pool	A vector giving a classification for pooling the sites in the species data. If missing, all sites are pooled together.
smallsample	Use small sample correction \((N-1)/N\), where \(N\) is the number of sites within the `pool`.
X, object	A `specpool` result object.
index	The selected index of extrapolated richness.
permutations	Usually an integer giving the number permutations, but can also be a list of control values for the permutations as returned by the function `how`, or a permutation matrix where each row gives the permuted indices.
minsize	Smallest number of sampling units reported.
parallel	Number of parallel processes or a predefined socket cluster. With `parallel = 1` uses ordinary, non-parallel processing. The parallel processing is done with parallel package.
display	Indices to be displayed.
alpha	Level of quantiles shown. This proportion will be left outside symmetric limits.
type	Type of graph produced in `xyplot`.
...	Other parameters (not used).

Details

Many species will always remain unseen or undetected in a collection of sample plots. The function uses some popular ways of estimating the number of these unseen species and adding them to the observed species richness (Palmer 1990, Colwell & Coddington 1994).

The incidence-based estimates in specpool use the frequencies of species in a collection of sites. In the following, \(S_P\) is the extrapolated richness in a pool, \(S_0\) is the observed number of species in the collection, \(a_1\) and \(a_2\) are the number of species occurring only in one or only in two sites in the collection, \(p_i\) is the frequency of species \(i\), and \(N\) is the number of sites in the collection. The variants of extrapolated richness in specpool are:

Chao	\(S_P = S_0 + \frac{a_1^2}{2 a_2}\frac{N-1}{N}\)
Chao bias-corrected	\(S_P = S_0 + \frac{a_1(a_1-1)}{2(a_2+1)} \frac{N-1}{N}\)
First order jackknife	\(S_P = S_0 + a_1 \frac{N-1}{N}\)
Second order jackknife	\(S_P = S_0 + a_1 \frac{2N - 3}{N} - a_2 \frac{(N-2)^2}{N (N-1)}\)
Bootstrap	\(S_P = S_0 + \sum_{i=1}^{S_0} (1 - p_i)^N\)

specpool normally uses basic Chao equation, but when there are no doubletons (\(a2=0\)) it switches to bias-corrected version. In that case the Chao equation simplifies to \(S_0 + \frac{1}{2} a_1 (a_1-1) \frac{N-1}{N}\).

The abundance-based estimates in estimateR use counts (numbers of individuals) of species in a single site. If called for a matrix or data frame, the function will give separate estimates for each site. The two variants of extrapolated richness in estimateR are bias-corrected Chao and ACE (O'Hara 2005, Chiu et al. 2014). The Chao estimate is similar as the bias corrected one above, but \(a_i\) refers to the number of species with abundance \(i\) instead of number of sites, and the small-sample correction is not used. The ACE estimate is defined as:

ACE	\(S_P = S_{abund} + \frac{S_{rare}}{C_{ace}}+ \frac{a_1}{C_{ace}} \gamma^2_{ace}\)
where	\(C_{ace} = 1 - \frac{a_1}{N_{rare}}\)
	\(\gamma^2_{ace} = \max \left[ \frac{S_{rare} \sum_{i=1}^{10} i(i-1)a_i}{C_{ace} N_{rare} (N_{rare} - 1)}-1, 0 \right]\)

Here \(a_i\) refers to number of species with abundance \(i\) and \(S_{rare}\) is the number of rare species, \(S_{abund}\) is the number of abundant species, with an arbitrary threshold of abundance 10 for rare species, and \(N_{rare}\) is the number of individuals in rare species.

Functions estimate the standard errors of the estimates. These only concern the number of added species, and assume that there is no variance in the observed richness. The equations of standard errors are too complicated to be reproduced in this help page, but they can be studied in the R source code of the function and are discussed in the vignette that can be read with the browseVignettes("vegan"). The standard error are based on the following sources: Chiu et al. (2014) for the Chao estimates and Smith and van Belle (1984) for the first-order Jackknife and the bootstrap (second-order jackknife is still missing). For the variance estimator of \(S_{ace}\) see O'Hara (2005).

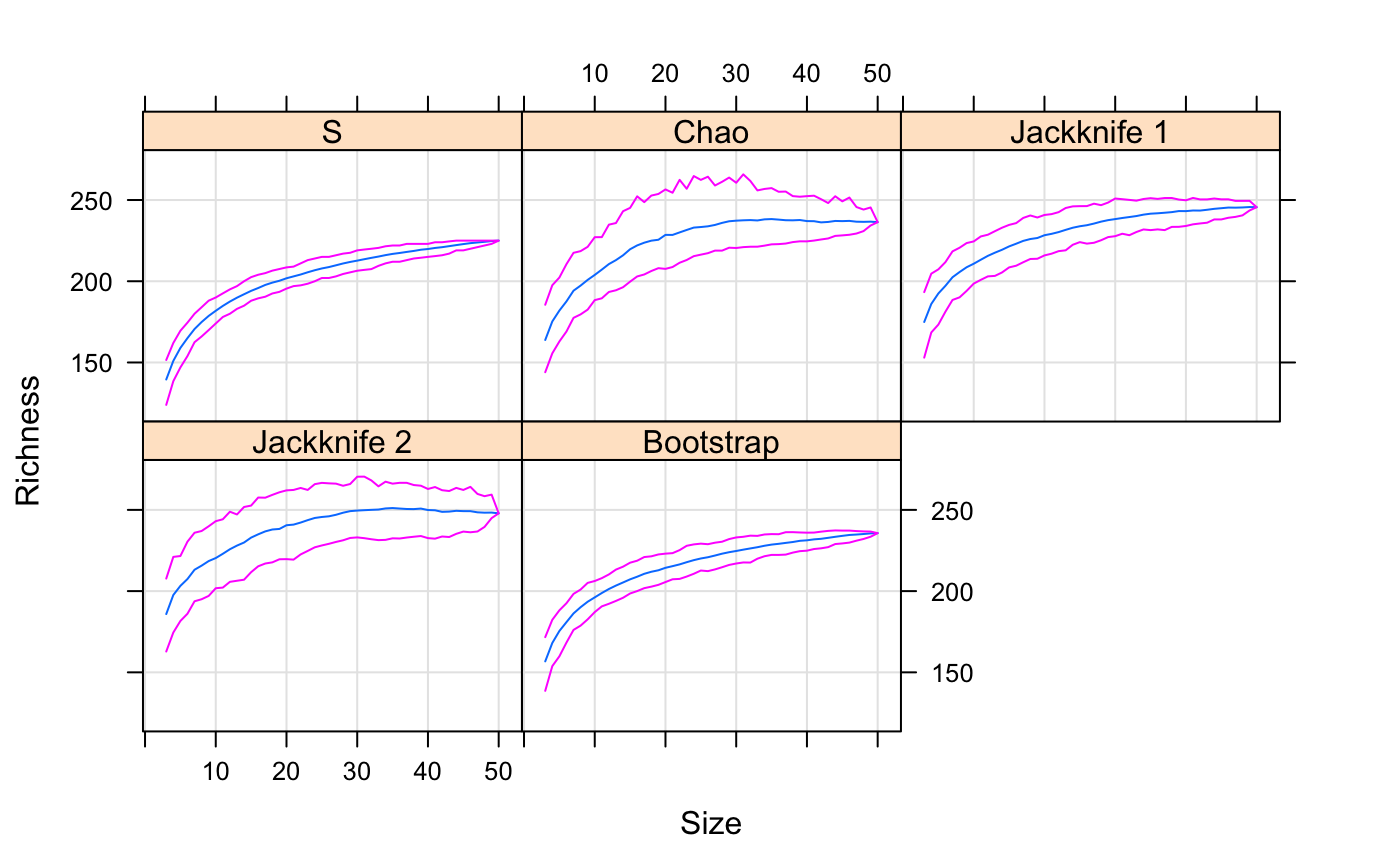
Functions poolaccum and estaccumR are similar to specaccum, but estimate extrapolated richness indices of specpool or estimateR in addition to number of species for random ordering of sampling units. Function specpool uses presence data and estaccumR count data. The functions share summary and plot methods. The summary returns quantile envelopes of permutations corresponding the given level of alpha and standard deviation of permutations for each sample size. NB., these are not based on standard deviations estimated within specpool or estimateR, but they are based on permutations. The plot function shows the mean and envelope of permutations with given alpha for models. The selection of models can be restricted and order changes using the display argument in summary or plot. For configuration of plot command, see xyplot.

Value

Function specpool returns a data frame with entries for observed richness and each of the indices for each class in pool vector. The utility function specpool2vect maps the pooled values into a vector giving the value of selected index for each original site. Function estimateR returns the estimates and their standard errors for each site. Functions poolaccum and estimateR return matrices of permutation results for each richness estimator, the vector of sample sizes and a table of means of permutations for each estimator.

References

Chao, A. (1987). Estimating the population size for capture-recapture data with unequal catchability. Biometrics 43, 783--791.

Chiu, C.H., Wang, Y.T., Walther, B.A. & Chao, A. (2014). Improved nonparametric lower bound of species richness via a modified Good-Turing frequency formula. Biometrics 70, 671--682.

Colwell, R.K. & Coddington, J.A. (1994). Estimating terrestrial biodiversity through extrapolation. Phil. Trans. Roy. Soc. London B 345, 101--118.

O'Hara, R.B. (2005). Species richness estimators: how many species can dance on the head of a pin? J. Anim. Ecol. 74, 375--386.

Palmer, M.W. (1990). The estimation of species richness by extrapolation. Ecology 71, 1195--1198.

Smith, E.P & van Belle, G. (1984). Nonparametric estimation of species richness. Biometrics 40, 119--129.

Note

The functions are based on assumption that there is a species pool: The community is closed so that there is a fixed pool size \(S_P\). In general, the functions give only the lower limit of species richness: the real richness is \(S >= S_P\), and there is a consistent bias in the estimates. Even the bias-correction in Chao only reduces the bias, but does not remove it completely (Chiu et al. 2014).

Optional small sample correction was added to specpool in vegan 2.2-0. It was not used in the older literature (Chao 1987), but it is recommended recently (Chiu et al. 2014).

See http://viceroy.eeb.uconn.edu/EstimateS for a more complete (and positive) discussion and alternative software for some platforms.

Examples

data(dune)
data(dune.env)
pool <- with(dune.env, specpool(dune, Management))
pool
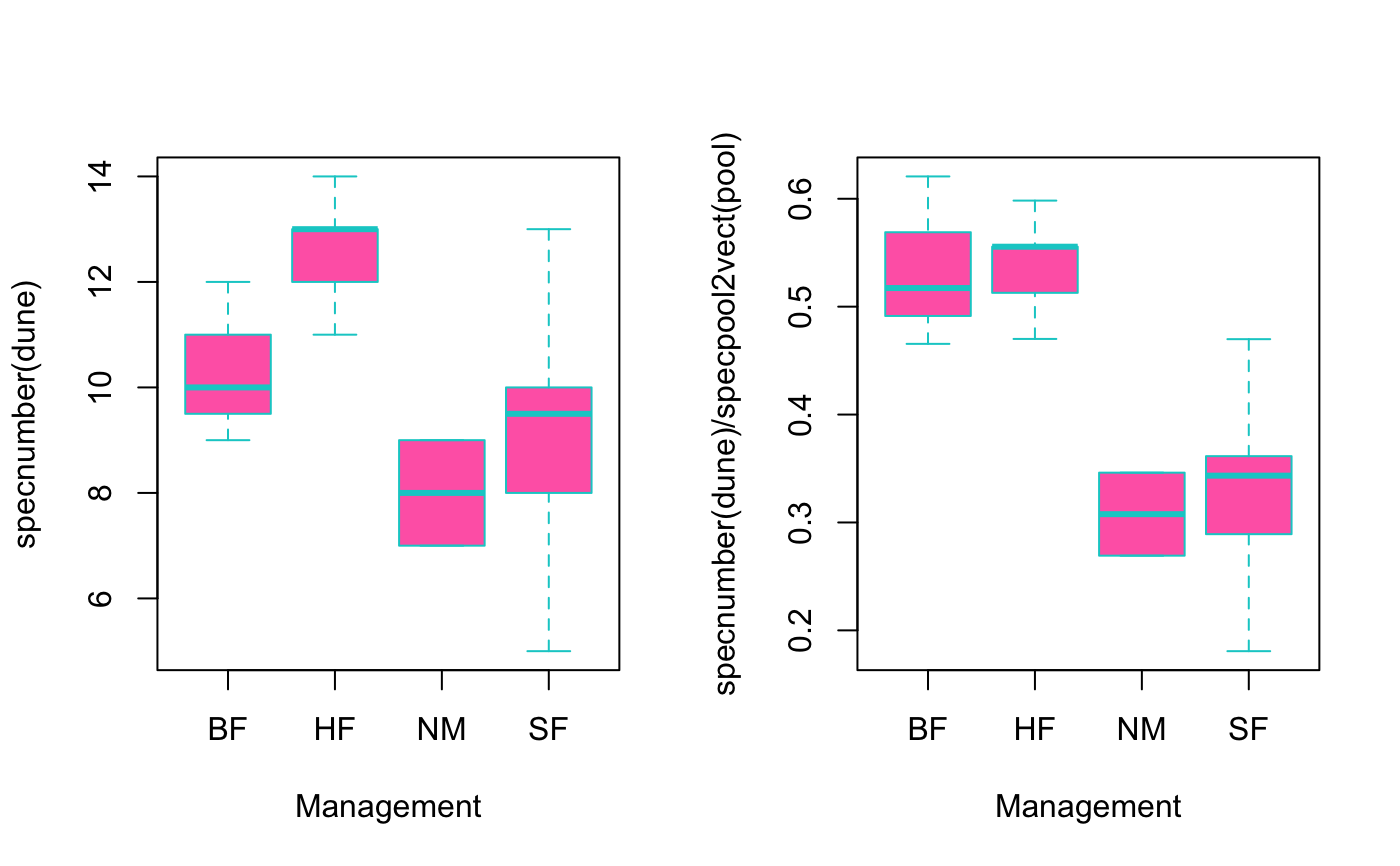
#>    Species     chao   chao.se    jack1 jack1.se    jack2     boot  boot.se n
#> BF      16 17.19048 1.5895675 19.33333 2.211083 19.83333 17.74074 1.646379 3
#> HF      21 21.51429 0.9511693 23.40000 1.876166 22.05000 22.56864 1.821518 5
#> NM      21 22.87500 2.1582871 26.00000 3.291403 25.73333 23.77696 2.300982 6
#> SF      21 29.88889 8.6447967 27.66667 3.496029 31.40000 23.99496 1.850288 6
op <- par(mfrow=c(1,2))
boxplot(specnumber(dune) ~ Management, data = dune.env,
        col = "hotpink", border = "cyan3")
boxplot(specnumber(dune)/specpool2vect(pool) ~ Management,
        data = dune.env, col = "hotpink", border = "cyan3")
par(op)
data(BCI)
## Accumulation model
pool <- poolaccum(BCI)
summary(pool, display = "chao")
#> $chao
#>        N     Chao     2.5%    97.5%   Std.Dev
#>  [1,]  3 163.8446 144.0081 185.5279 11.425025
#>  [2,]  4 175.2613 155.6339 197.5430 11.102676
#>  [3,]  5 181.9404 162.9204 202.2775 10.225221
#>  [4,]  6 187.5935 169.0500 210.5131 10.905422
#>  [5,]  7 194.1845 177.4721 217.4949 10.937797
#>  [6,]  8 197.3287 179.5973 218.5361 10.734286
#>  [7,]  9 200.8372 182.5336 221.1848 10.414775
#>  [8,] 10 203.8975 188.3830 227.1169 11.934209
#>  [9,] 11 207.1645 189.4961 227.1497 11.434965
#> [10,] 12 210.5631 193.3939 234.8315 12.642137
#> [11,] 13 213.0122 194.4495 235.8226 10.466458
#> [12,] 14 215.9590 196.3256 243.0967 12.638403
#> [13,] 15 219.7021 199.7543 245.1639 12.620668
#> [14,] 16 222.0587 202.9523 252.2632 13.257926
#> [15,] 17 223.7354 204.1720 248.6958 12.406220
#> [16,] 18 224.9768 206.3021 252.7272 11.918966
#> [17,] 19 225.5385 208.0477 253.7259 11.703422
#> [18,] 20 228.5411 207.6179 256.5100 12.553768
#> [19,] 21 228.5166 208.7494 254.4789 11.392270
#> [20,] 22 230.0595 211.3889 262.4102 12.168649
#> [21,] 23 231.5704 213.0775 256.9304 12.111100
#> [22,] 24 233.0244 215.4363 264.7362 12.350755
#> [23,] 25 233.3699 216.3727 262.3983 11.615367
#> [24,] 26 233.8105 217.2809 264.3478 11.762489
#> [25,] 27 234.6579 218.8600 258.9373 11.089195
#> [26,] 28 235.9213 218.8506 261.2105 11.145760
#> [27,] 29 236.9192 220.6398 263.8172 10.841831
#> [28,] 30 237.2869 220.4688 260.6325 10.824935
#> [29,] 31 237.5111 220.9968 265.7840 11.470647
#> [30,] 32 237.6487 221.2487 261.7231 10.944063
#> [31,] 33 237.4202 221.2689 255.9092  9.477793
#> [32,] 34 238.0942 221.9147 256.8135  9.768634
#> [33,] 35 238.2695 222.7146 257.3221  9.324122
#> [34,] 36 237.9344 222.8572 255.0762  8.983655
#> [35,] 37 237.5586 223.2032 255.2048  8.608156
#> [36,] 38 237.5008 224.1010 252.4009  8.116407
#> [37,] 39 237.6810 224.5726 252.0271  7.319545
#> [38,] 40 237.0329 224.5498 252.3750  7.080692
#> [39,] 41 236.9653 225.0362 252.6562  6.834743
#> [40,] 42 236.2359 225.7095 250.5005  6.085949
#> [41,] 43 236.5034 226.3343 248.1269  6.168847
#> [42,] 44 237.1143 227.9140 252.3150  6.207299
#> [43,] 45 237.0079 228.2277 249.1699  5.438751
#> [44,] 46 237.1486 228.6086 251.5188  5.215137
#> [45,] 47 236.6522 229.3700 245.6755  3.889002
#> [46,] 48 236.5599 230.8615 244.1243  3.204779
#> [47,] 49 236.6752 234.3115 245.4082  2.331291
#> [48,] 50 236.3732 236.3732 236.3732  0.000000
#> 
#> attr(,"class")
#> [1] "summary.poolaccum"
plot(pool)
## Quantitative model
estimateR(BCI[1:5,])
#>                   1          2          3          4          5
#> S.obs     93.000000  84.000000  90.000000  94.000000 101.000000
#> S.chao1  117.473684 117.214286 141.230769 111.550000 136.000000
#> se.chao1  11.583785  15.918953  23.001405   8.919663  15.467344
#> S.ACE    122.848959 117.317307 134.669844 118.729941 137.114088
#> se.ACE     5.736054   5.571998   6.191618   5.367571   5.848474