Additive Diversity Partitioning and Hierarchical Null Model Testing

In additive diversity partitioning, mean values of alpha diversity at lower levels of a sampling hierarchy are compared to the total diversity in the entire data set (gamma diversity). In hierarchical null model testing, a statistic returned by a function is evaluated according to a nested hierarchical sampling design (hiersimu).

adipart(...)
# S3 method for default
adipart(y, x, index=c("richness", "shannon", "simpson"),
    weights=c("unif", "prop"), relative = FALSE, nsimul=99,
    method = "r2dtable", ...)
# S3 method for formula
adipart(formula, data, index=c("richness", "shannon", "simpson"),
    weights=c("unif", "prop"), relative = FALSE, nsimul=99,
    method = "r2dtable", ...)

hiersimu(...)
# S3 method for default
hiersimu(y, x, FUN, location = c("mean", "median"),
    relative = FALSE, drop.highest = FALSE, nsimul=99,
    method = "r2dtable", ...)
# S3 method for formula
hiersimu(formula, data, FUN, location = c("mean", "median"),
    relative = FALSE, drop.highest = FALSE, nsimul=99,
    method = "r2dtable", ...)

Arguments

y	A community matrix.
x	A matrix with same number of rows as in `y`, columns coding the levels of sampling hierarchy. The number of groups within the hierarchy must decrease from left to right. If `x` is missing, function performs an overall decomposition into alpha, beta and gamma diversities.
formula	A two sided model formula in the form `y ~ x`, where `y` is the community data matrix with samples as rows and species as column. Right hand side (`x`) must be grouping variables referring to levels of sampling hierarchy, terms from right to left will be treated as nested (first column is the lowest, last is the highest level, at least two levels specified). Interaction terms are not allowed.
data	A data frame where to look for variables defined in the right hand side of `formula`. If missing, variables are looked in the global environment.
index	Character, the diversity index to be calculated (see Details).
weights	Character, `"unif"` for uniform weights, `"prop"` for weighting proportional to sample abundances to use in weighted averaging of individual alpha values within strata of a given level of the sampling hierarchy.
relative	Logical, if `TRUE` then alpha and beta diversity values are given relative to the value of gamma for function `adipart`.
nsimul	Number of permutations to use. If `nsimul = 0`, only the `FUN` argument is evaluated. It is thus possible to reuse the statistic values without a null model.
method	Null model method: either a name (character string) of a method defined in `make.commsim` or a `commsim` function. The default `"r2dtable"` keeps row sums and column sums fixed. See `oecosimu` for Details and Examples.
FUN	A function to be used by `hiersimu`. This must be fully specified, because currently other arguments cannot be passed to this function via `...`.
location	Character, identifies which function (mean or median) is to be used to calculate location of the samples.
drop.highest	Logical, to drop the highest level or not. When `FUN` evaluates only arrays with at least 2 dimensions, highest level should be dropped, or not selected at all.
...	Other arguments passed to functions, e.g. base of logarithm for Shannon diversity, or `method`, `thin` or `burnin` arguments for `oecosimu`.

Details

Additive diversity partitioning means that mean alpha and beta diversities add up to gamma diversity, thus beta diversity is measured in the same dimensions as alpha and gamma (Lande 1996). This additive procedure is then extended across multiple scales in a hierarchical sampling design with $i = 1, 2, 3, \ldots, m$ levels of sampling (Crist et al. 2003). Samples in lower hierarchical levels are nested within higher level units, thus from $i=1$ to $i=m$ grain size is increasing under constant survey extent. At each level $i$, $\alpha_i$ denotes average diversity found within samples.

At the highest sampling level, the diversity components are calculated as $$\beta_m = \gamma - \alpha_m$$ For each lower sampling level as $$\beta_i = \alpha_{i+1} - \alpha_i$$ Then, the additive partition of diversity is $$\gamma = \alpha_1 + \sum_{i=1}^m \beta_i$$

Average alpha components can be weighted uniformly (weight="unif") to calculate it as simple average, or proportionally to sample abundances (weight="prop") to calculate it as weighted average as follows $$\alpha_i = \sum_{j=1}^{n_i} D_{ij} w_{ij}$$ where $D_{ij}$ is the diversity index and $w_{ij}$ is the weight calculated for the $j$th sample at the $i$th sampling level.

The implementation of additive diversity partitioning in adipart follows Crist et al. 2003. It is based on species richness ($S$, not $S-1$), Shannon's and Simpson's diversity indices stated as the index argument.

The expected diversity components are calculated nsimul times by individual based randomisation of the community data matrix. This is done by the "r2dtable" method in oecosimu by default.

hiersimu works almost in the same way as adipart, but without comparing the actual statistic values returned by FUN to the highest possible value (cf. gamma diversity). This is so, because in most of the cases, it is difficult to ensure additive properties of the mean statistic values along the hierarchy.

Value

An object of class "adipart" or "hiersimu" with same structure as oecosimu objects.

References

Crist, T.O., Veech, J.A., Gering, J.C. and Summerville, K.S. (2003). Partitioning species diversity across landscapes and regions: a hierarchical analysis of $\alpha$, $\beta$, and $\gamma$-diversity. Am. Nat., 162, 734--743.

Lande, R. (1996). Statistics and partitioning of species diversity, and similarity among multiple communities. Oikos, 76, 5--13.

Examples

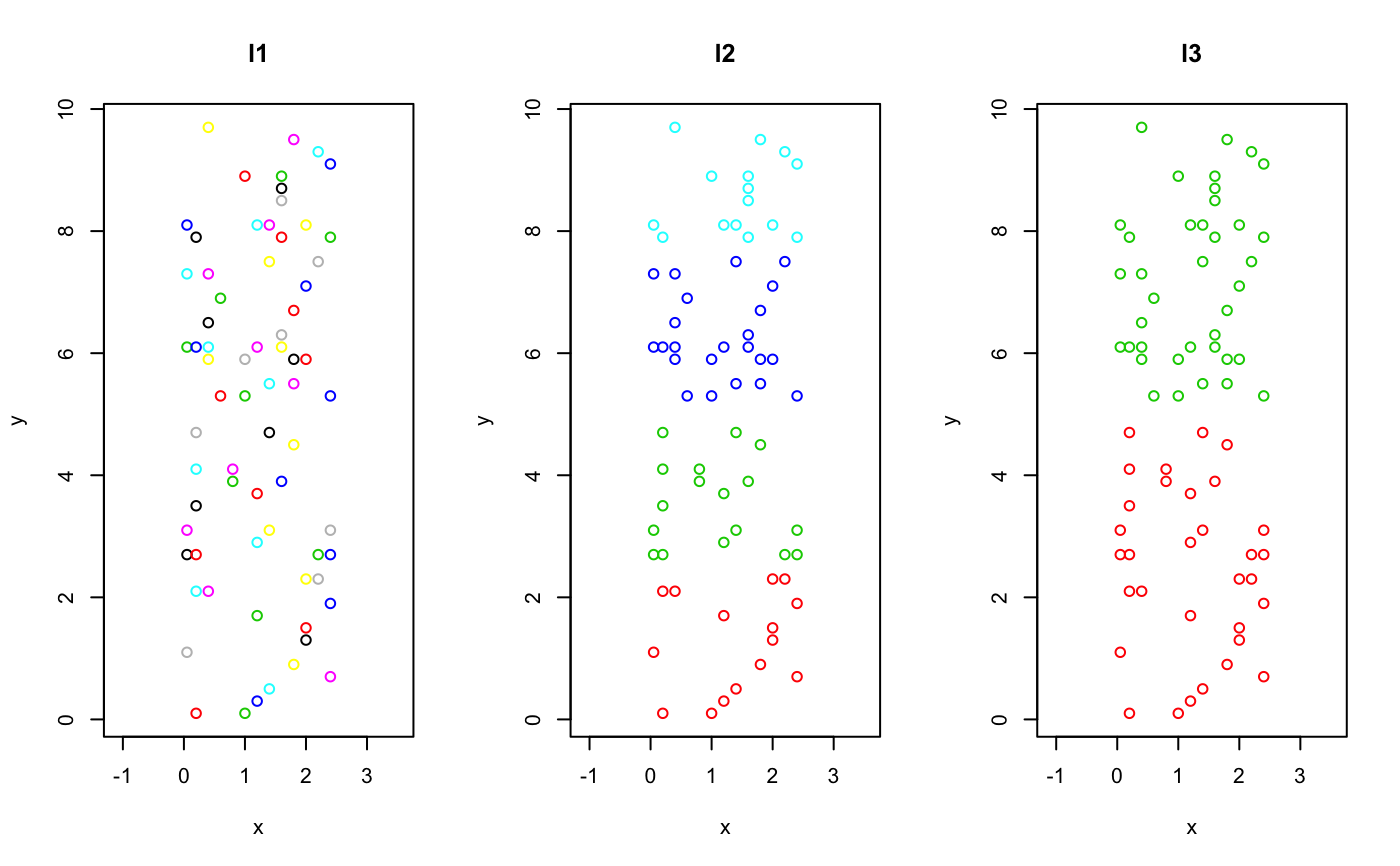
## NOTE: 'nsimul' argument usually needs to be >= 99
## here much lower value is used for demonstration

data(mite)
data(mite.xy)
data(mite.env)
## Function to get equal area partitions of the mite data
cutter <- function (x, cut = seq(0, 10, by = 2.5)) {
    out <- rep(1, length(x))
    for (i in 2:(length(cut) - 1))
        out[which(x > cut[i] & x <= cut[(i + 1)])] <- i
    return(out)}
## The hierarchy of sample aggregation
levsm <- with(mite.xy, data.frame(
    l1=1:nrow(mite),
    l2=cutter(y, cut = seq(0, 10, by = 2.5)),
    l3=cutter(y, cut = seq(0, 10, by = 5)),
    l4=cutter(y, cut = seq(0, 10, by = 10))))
## Let's see in a map
par(mfrow=c(1,3))
plot(mite.xy, main="l1", col=as.numeric(levsm$l1)+1, asp = 1)
plot(mite.xy, main="l2", col=as.numeric(levsm$l2)+1, asp = 1)
plot(mite.xy, main="l3", col=as.numeric(levsm$l3)+1, asp = 1)
par(mfrow=c(1,1))
## Additive diversity partitioning
adipart(mite, index="richness", nsimul=19)
#> adipart object
#> 
#> Call: adipart(y = mite, index = "richness", nsimul = 19)
#> 
#> nullmodel method ‘r2dtable’ with 19 simulations
#> options:  index richness, weights unif
#> alternative hypothesis: statistic is less or greater than simulated values
#> 
#>         statistic     SES   mean   2.5%    50%  97.5% Pr(sim.)  
#> alpha.1    15.114 -36.377 22.374 22.088 22.343 22.834     0.05 *
#> gamma      35.000   0.000 35.000 35.000 35.000 35.000     1.00  
#> beta.1     19.886  36.377 12.626 12.166 12.657 12.912     0.05 *
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
adipart(mite ~ ., levsm, index="richness", nsimul=19)
#> adipart object
#> 
#> Call: adipart(formula = mite ~ ., data = levsm, index = "richness",
#> nsimul = 19)
#> 
#> nullmodel method ‘r2dtable’ with 19 simulations
#> options:  index richness, weights unif
#> alternative hypothesis: statistic is less or greater than simulated values
#> 
#>         statistic      SES     mean     2.5%      50%  97.5% Pr(sim.)  
#> alpha.1    15.114 -36.4611 22.34060 22.03214 22.35714 22.639     0.05 *
#> alpha.2    29.750 -24.5197 34.84211 34.50000 35.00000 35.000     0.05 *
#> alpha.3    33.000   0.0000 35.00000 35.00000 35.00000 35.000     0.05 *
#> gamma      35.000   0.0000 35.00000 35.00000 35.00000 35.000     1.00  
#> beta.1     14.636   6.9804 12.50150 11.95571 12.50714 12.942     0.05 *
#> beta.2      3.250  14.8892  0.15789  0.00000  0.00000  0.500     0.05 *
#> beta.3      2.000   0.0000  0.00000  0.00000  0.00000  0.000     0.05 *
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
## Hierarchical null model testing
## diversity analysis (similar to adipart)
hiersimu(mite, FUN=diversity, relative=TRUE, nsimul=19)
#> hiersimu object
#> 
#> Call: hiersimu(y = mite, FUN = diversity, relative = TRUE, nsimul = 19)
#> 
#> nullmodel method ‘r2dtable’ with 19 simulations
#> 
#> alternative hypothesis: statistic is less or greater than simulated values
#> 
#>         statistic     SES    mean    2.5%     50%  97.5% Pr(sim.)  
#> level_1   0.76064 -75.754 0.93930 0.93512 0.93945 0.9428     0.05 *
#> leve_2    1.00000   0.000 1.00000 1.00000 1.00000 1.0000     1.00  
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
hiersimu(mite ~., levsm, FUN=diversity, relative=TRUE, nsimul=19)
#> hiersimu object
#> 
#> Call: hiersimu(formula = mite ~ ., data = levsm, FUN = diversity,
#> relative = TRUE, nsimul = 19)
#> 
#> nullmodel method ‘r2dtable’ with 19 simulations
#> 
#> alternative hypothesis: statistic is less or greater than simulated values
#> 
#>    statistic      SES    mean    2.5%     50%  97.5% Pr(sim.)  
#> l1   0.76064  -70.226 0.93931 0.93495 0.93987 0.9438     0.05 *
#> l2   0.89736 -216.285 0.99811 0.99740 0.99807 0.9989     0.05 *
#> l3   0.92791 -476.160 0.99936 0.99911 0.99938 0.9996     0.05 *
#> l4   1.00000    0.000 1.00000 1.00000 1.00000 1.0000     1.00  
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
## Hierarchical testing with the Morisita index
morfun <- function(x) dispindmorisita(x)$imst
hiersimu(mite ~., levsm, morfun, drop.highest=TRUE, nsimul=19)
#> hiersimu object
#> 
#> Call: hiersimu(formula = mite ~ ., data = levsm, FUN = morfun,
#> drop.highest = TRUE, nsimul = 19)
#> 
#> nullmodel method ‘r2dtable’ with 19 simulations
#> 
#> alternative hypothesis: statistic is less or greater than simulated values
#> 
#>    statistic     SES      mean      2.5%       50%   97.5% Pr(sim.)  
#> l1   0.52070  5.2935  0.361706  0.319017  0.362010  0.4080     0.05 *
#> l2   0.60234 12.1078  0.142990  0.056482  0.148891  0.1905     0.05 *
#> l3   0.67509 18.3684 -0.212835 -0.269210 -0.222593 -0.1226     0.05 *
#> ---
#> Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Additive Diversity Partitioning and Hierarchical Null Model Testing

Arguments

Details

Value

References

See also

Examples

Contents

Author